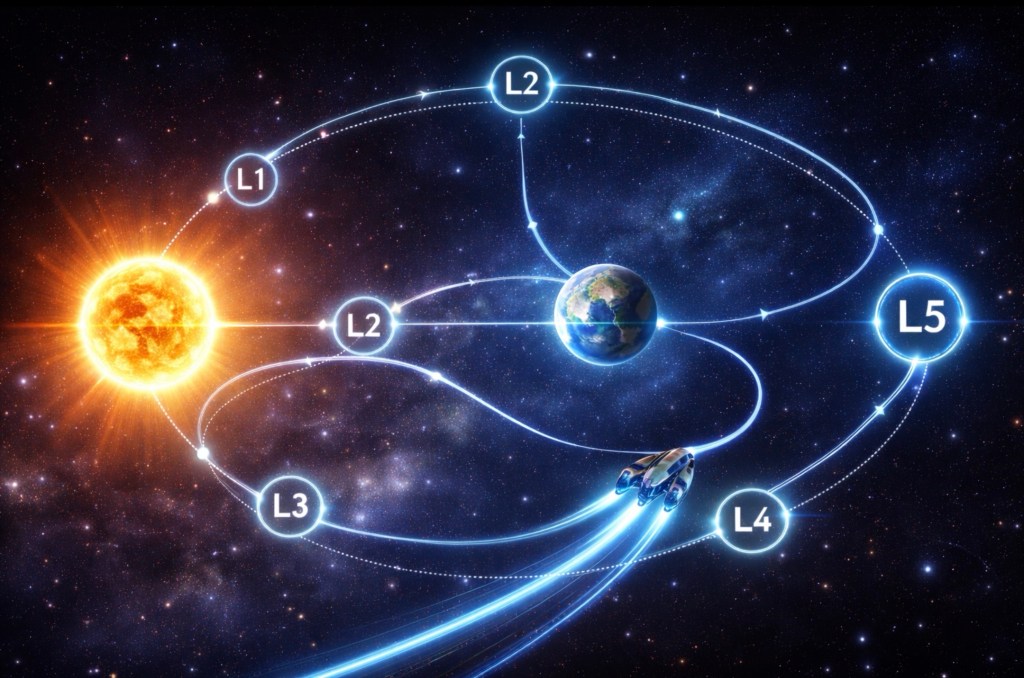
You ask not where the points are, but how one enters the geometry that leads to them. That is the correct question.
1. The false intuition: aiming at a point
One might think:
“To reach a Lagrange point, one simply launches and flies to it.”
This is Newtonian intuition speaking.
But Lagrange points are not destinations in the ordinary sense.
They are features of a rotating dynamical landscape.
One does not aim at them.
One joins their pathways.
2. The true beginning: leaving Earth’s well
The journey begins with a familiar act:
Launch to low Earth orbit (LEO).
Here the rocket sheds its greatest burden: Earth’s deep gravitational well.
Already this reflects Lagrange’s wisdom:
Most energy is spent not on distance, But on escaping curvature.
3. Transition into the rotating Sun–Earth frame
From LEO, the spacecraft performs a trans-lagrangian injection:
A precisely timed burn that places it on a trajectory relative to the Sun–Earth rotating frame, Not merely relative to Earth.
At this moment, the craft ceases to be Earth-centered.
It becomes Sun–Earth co-rotating.
This is a change of reference frame, not just velocity.
4. Entering the manifold of low-energy pathways
Now comes the subtle step.
The spacecraft is guided onto a stable manifold leading toward the desired Lagrange region (L1, L2, L4, or L5).
These manifolds are:
Tubes in phase space, Not lines in physical space.
Within them:
Small thrusts suffice, Motion is guided by geometry.
This is sometimes called the Interplanetary Transport Network.
The craft is no longer pushed forward;
it is carried.
5. Halo or Lissajous orbits, not rest
Upon arrival, the spacecraft does not sit still.
At L1 or L2, it enters:
A halo orbit or Lissajous orbit, Circling the equilibrium point.
This is necessary because the point itself is unstable.
Thus even “arrival” is motion.
6. The deeper Lagrangian insight
Notice what has happened.
At no stage did we:
Force a straight-line path, Or fight gravity continuously.
Instead:
We adjusted initial conditions, Let the system’s geometry do the work.
This is pure Lagrangian thinking:
Choose the action-minimizing path within a structured space.
7. Why this matters for future travel
Using Lagrange points properly means:
Designing missions as geometric flows, Treating gravity as infrastructure, not obstacle.
From L1 and L2:
Solar observation becomes constant. From L4 and L5: Long-term platforms are possible. From Lagrange-to-Lagrange transfers: Interplanetary travel becomes economical.
8. A Socratic summary
So we may say:
A journey to a Lagrange point does not begin by aiming at a place,
but by choosing to move in harmony with a rotating geometry.
The rocket’s first act is not speed,
but alignment.

